biweight_midvariance¶

astropy.stats.biweight_midvariance(a, c=9.0, M=None)[source] [edit on github]¶

Compute the biweight midvariance for an array.

Returns the biweight midvariance for the array elements. The biweight midvariance is a robust statistic for determining the midvariance (i.e. the standard deviation) of a distribution.

The biweight location is given by the following equation

$C_{bl}= n^{1/2} \frac{[\Sigma_{|u_i|<1} (x_i-M)**2(1-u_i^2)^4]^{0.5}} {|\Sigma_{|u_i|<1} (1-u_i^2)(1-5u_i^2)|}$

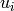where $u_i$ is given by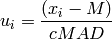

$u_{i} = \frac{(x_i-M)}{cMAD}$

where MAD is the median absolute deviation. For the midvariance parameter, c is typically uses a value of 9.0.

For more details, see Beers, Flynn, and Gebhardt, 1990, AJ, 100, 32B

Parameters:

a : array_like

Input array or object that can be converted to an array.

c : float

Tuning constant for the biweight estimator. Default value is 9.0.

M : float, optional

Initial gues for the biweight location.

Returns:

biweight_midvariance : float

Returns the biweight midvariance for the array elements.

Examples

This will generate random variates from a Gaussian distribution and return the median absolute deviation for that distribution:

>>> from astropy.stats.funcs import biweight_midvariance
>>> from numpy.random import randn
>>> randvar = randn(10000)
>>> scl = biweight_midvariance(randvar)

Navigation

biweight_midvariance¶

Page Contents