Example: Defining A Coordinate Frame for the Sgr Dwarf¶

This document describes in detail how to subclass and define a custom spherical coordinate frame, as discussed in Using and Designing Coordinate Frames and the docstring for BaseCoordinateFrame. In this example, we will define a coordinate system defined by the plane of orbit of the Sagittarius Dwarf Galaxy (hereafter Sgr; as defined in Majewski et al. 2003). The Sgr coordinate system is often referred to in terms of two angular coordinates, 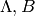$\Lambda,B$ .

We need to define a subclass of BaseCoordinateFrame that knows the names and units of the coordinate system angles in each of the supported representations. In this case we support SphericalRepresentation with “Lambda” and “Beta”. Then we have to define the transformation from this coordinate system to some other built-in system. Here we will use Galactic coordinates, represented by the Galactic class.

The first step is to create a new class, which we’ll call Sagittarius and make it a subclass of BaseCoordinateFrame:

import numpy as np
from numpy import cos, sin

from astropy.coordinates import frame_transform_graph
from astropy.coordinates.angles import rotation_matrix
import astropy.coordinates as coord
import astropy.units as u

class Sagittarius(coord.BaseCoordinateFrame):
    """
    A Heliocentric spherical coordinate system defined by the orbit
    of the Sagittarius dwarf galaxy, as described in
        http://adsabs.harvard.edu/abs/2003ApJ...599.1082M
    and further explained in
        http://www.astro.virginia.edu/~srm4n/Sgr/.

    Parameters
    ----------
    representation : `BaseRepresentation` or None
        A representation object or None to have no data (or use the other keywords)
    Lambda : `Angle`, optional, must be keyword
        The longitude-like angle corresponding to Sagittarius' orbit.
    Beta : `Angle`, optional, must be keyword
        The latitude-like angle corresponding to Sagittarius' orbit.
    distance : `Quantity`, optional, must be keyword
        The Distance for this object along the line-of-sight.

    """
    default_representation = coord.SphericalRepresentation

    frame_specific_representation_info = {
        'spherical': [coord.RepresentationMapping('lon', 'Lambda'),
                      coord.RepresentationMapping('lat', 'Beta'),
                      coord.RepresentationMapping('distance', 'distance')],
        'unitspherical': [coord.RepresentationMapping('lon', 'Lambda'),
                          coord.RepresentationMapping('lat', 'Beta')]
    }

Line by line, the first few are simply imports. Next we define the class as a subclass of BaseCoordinateFrame. Then we include a descriptive docstring. The final lines are class-level attributes that specify the default representation for the data and mappings from the attribute names used by representation objects to the names that are to be used by Sagittarius. In this case we override the names in the spherical representations but don’t do anything with other representations like cartesian or cylindrical.

Next we have to define the transformation to some other built-in coordinate system; we will use Galactic coordinates. We can do this by defining functions that return transformation matrices, or by simply defining a function that accepts a coordinate and returns a new coordinate in the new system. We’ll start by constructing the rotation matrix, using the helper function rotation_matrix:

# Define the Euler angles (from Law & Majewski 2010)
SGR_PHI = np.radians(180+3.75)
SGR_THETA = np.radians(90-13.46)
SGR_PSI = np.radians(180+14.111534)

# Generate the rotation matrix using the x-convention (see Goldstein)
D = rotation_matrix(SGR_PHI, "z", unit=u.radian)
C = rotation_matrix(SGR_THETA, "x", unit=u.radian)
B = rotation_matrix(SGR_PSI, "z", unit=u.radian)
SGR_MATRIX = np.array(B.dot(C).dot(D))

This is done at the module level, since it will be used by both the transformation from Sgr to Galactic as well as the inverse from Galactic to Sgr. Now we can define our first transformation function:

# Galactic to Sgr coordinates
@frame_transform_graph.transform(coord.FunctionTransform, coord.Galactic, Sagittarius)
def galactic_to_sgr(gal_coord, sgr_frame):
    """ Compute the transformation from Galactic spherical to
        heliocentric Sgr coordinates.
    """

    l = np.atleast_1d(gal_coord.l.radian)
    b = np.atleast_1d(gal_coord.b.radian)

    X = np.cos(b)*np.cos(l)
    Y = np.cos(b)*np.sin(l)
    Z = np.sin(b)

    # Calculate X,Y,Z,distance in the Sgr system
    Xs, Ys, Zs = SGR_MATRIX.dot(np.array([X, Y, Z]))
    Zs = -Zs

    # Calculate the angular coordinates lambda,beta
    Lambda = np.arctan2(Ys,Xs)*u.radian
    Lambda[Lambda < 0] = Lambda[Lambda < 0] + 2.*np.pi*u.radian
    Beta = np.arcsin(Zs/np.sqrt(Xs*Xs+Ys*Ys+Zs*Zs))*u.radian

    return Sagittarius(Lambda=Lambda, Beta=Beta,
                       distance=gal_coord.distance)

The decorator @frame_transform_graph.transform(coord.FunctionTransform, coord.Galactic, Sagittarius) registers this function on the frame_transform_graph as a transformation. Inside the function, we simply follow the same procedure as detailed by David Law’s transformation code. Note that in this case, both coordinate systems are heliocentric, so we can simply copy any distance from the Galactic object.

We then register the inverse transformation by using the transpose of the rotation matrix (which is faster to compute than the inverse):

# Sgr to Galactic coordinates
@frame_transform_graph.transform(coord.FunctionTransform, Sagittarius, coord.Galactic)
def sgr_to_galactic(sgr_coord, gal_frame):
    """ Compute the transformation from heliocentric Sgr coordinates to
        spherical Galactic.
    """
    L = np.atleast_1d(sgr_coord.Lambda.radian)
    B = np.atleast_1d(sgr_coord.Beta.radian)

    Xs = cos(B)*cos(L)
    Ys = cos(B)*sin(L)
    Zs = sin(B)
    Zs = -Zs

    X, Y, Z = SGR_MATRIX.T.dot(np.array([Xs, Ys, Zs]))

    l = np.arctan2(Y,X)*u.radian
    b = np.arcsin(Z/np.sqrt(X*X+Y*Y+Z*Z))*u.radian

    l[l<=0] += 2*np.pi*u.radian

    return coord.Galactic(l=l, b=b, distance=sgr_coord.distance)

Now that we’ve registered these transformations between Sagittarius and Galactic, we can transform between any coordinate system and Sagittarius (as long as the other system has a path to transform to Galactic). For example, to transform from ICRS coordinates to Sagittarius, we simply:

>>> import astropy.units as u
>>> import astropy.coordinates as coord
>>> icrs = coord.ICRS(280.161732*u.degree, 11.91934*u.degree)
>>> icrs.transform_to(Sagittarius)  
<Sagittarius Coordinate: (Lambda, Beta, distance) in (deg, deg, )
    (346.818273..., -39.283667..., 1.0)>

The complete code for the above example is included below for reference.

Complete Code for Example¶

# coding: utf-8

""" Astropy coordinate class for the Sagittarius coordinate system """

from __future__ import division, print_function

__author__ = "adrn <adrn@astro.columbia.edu>"

# Third-party
import numpy as np
from numpy import cos, sin

from astropy.coordinates import frame_transform_graph
from astropy.coordinates.angles import rotation_matrix
import astropy.coordinates as coord
import astropy.units as u


__all__ = ["Sagittarius"]


class Sagittarius(coord.BaseCoordinateFrame):
    """
    A Heliocentric spherical coordinate system defined by the orbit
    of the Sagittarius dwarf galaxy, as described in
        http://adsabs.harvard.edu/abs/2003ApJ...599.1082M
    and further explained in
        http://www.astro.virginia.edu/~srm4n/Sgr/.

    Parameters
    ----------
    representation : `BaseRepresentation` or None
        A representation object or None to have no data (or use the other keywords)
    Lambda : `Angle`, optional, must be keyword
        The longitude-like angle corresponding to Sagittarius' orbit.
    Beta : `Angle`, optional, must be keyword
        The latitude-like angle corresponding to Sagittarius' orbit.
    distance : `Quantity`, optional, must be keyword
        The Distance for this object along the line-of-sight.

    """
    default_representation = coord.SphericalRepresentation

    frame_specific_representation_info = {
        'spherical': [coord.RepresentationMapping('lon', 'Lambda'),
                      coord.RepresentationMapping('lat', 'Beta'),
                      coord.RepresentationMapping('distance', 'distance')],
        'unitspherical': [coord.RepresentationMapping('lon', 'Lambda'),
                          coord.RepresentationMapping('lat', 'Beta')]
    }

# Define the Euler angles (from Law & Majewski 2010)
phi = np.radians(180+3.75)
theta = np.radians(90-13.46)
psi = np.radians(180+14.111534)

# Generate the rotation matrix using the x-convention (see Goldstein)
D = rotation_matrix(phi, "z", unit=u.radian)
C = rotation_matrix(theta, "x", unit=u.radian)
B = rotation_matrix(psi, "z", unit=u.radian)
sgr_matrix = np.array(B.dot(C).dot(D))


# Galactic to Sgr coordinates
@frame_transform_graph.transform(coord.FunctionTransform, coord.Galactic, Sagittarius)
def galactic_to_sgr(gal_coord, sgr_frame):
    """ Compute the transformation from Galactic spherical to
        heliocentric Sgr coordinates.
    """

    l = np.atleast_1d(gal_coord.l.radian)
    b = np.atleast_1d(gal_coord.b.radian)

    X = cos(b)*cos(l)
    Y = cos(b)*sin(l)
    Z = sin(b)

    # Calculate X,Y,Z,distance in the Sgr system
    Xs, Ys, Zs = sgr_matrix.dot(np.array([X, Y, Z]))
    Zs = -Zs

    # Calculate the angular coordinates lambda,beta
    Lambda = np.arctan2(Ys, Xs)*u.radian
    Lambda[Lambda < 0] = Lambda[Lambda < 0] + 2.*np.pi*u.radian
    Beta = np.arcsin(Zs/np.sqrt(Xs*Xs+Ys*Ys+Zs*Zs))*u.radian

    return Sagittarius(Lambda=Lambda, Beta=Beta,
                       distance=gal_coord.distance)


# Sgr to Galactic coordinates
@frame_transform_graph.transform(coord.FunctionTransform, Sagittarius, coord.Galactic)
def sgr_to_galactic(sgr_coord, gal_frame):
    """ Compute the transformation from heliocentric Sgr coordinates to
        spherical Galactic.
    """
    L = np.atleast_1d(sgr_coord.Lambda.radian)
    B = np.atleast_1d(sgr_coord.Beta.radian)

    Xs = cos(B)*cos(L)
    Ys = cos(B)*sin(L)
    Zs = sin(B)
    Zs = -Zs

    X, Y, Z = sgr_matrix.T.dot(np.array([Xs, Ys, Zs]))

    l = np.arctan2(Y, X)*u.radian
    b = np.arcsin(Z/np.sqrt(X*X+Y*Y+Z*Z))*u.radian

    l[l<0] += 2*np.pi*u.radian

    return coord.Galactic(l=l, b=b, distance=sgr_coord.distance)

if __name__ == "__main__":
    # Example use case for our newly defined coordinate class
    icrs = coord.ICRS(152.88572*u.degree, 11.57281*u.degree)
    sgr = icrs.transform_to(Sagittarius)
    print(sgr)

Example: Defining A Coordinate Frame for the Sgr Dwarf¶

See Also¶

Complete Code for Example¶

Page Contents

Navigation

Example: Defining A Coordinate Frame for the Sgr Dwarf¶

See Also¶

Complete Code for Example¶

Page Contents